能带弯曲(Band bending)
最近有一个实验的合作涉及到能带弯曲,在知乎以及Physics of Semiconductor Devices这本教材上学习了一下记一下笔记。
半导体能带在半导体和金属接触时,表面处发生弯曲,这种现象称为“能带弯曲”。
其中有两种接触方式:肖特基接触 和 欧姆接触
对于我们所研究的 $\rm Au/TiO_2$ 体系,金属和n型半导体的接触,就属于肖特基接触
金属功函数大于n型半导体,即($\phi_m > \phi_s$)
功函数定义为费米能级与真空能级之间的能量差,简单理解为“让电子逃离材料表面所需要的能量”,这里金属的功函数比半导体的大,那么电子会从半导体流向金属,直到两者达到平衡。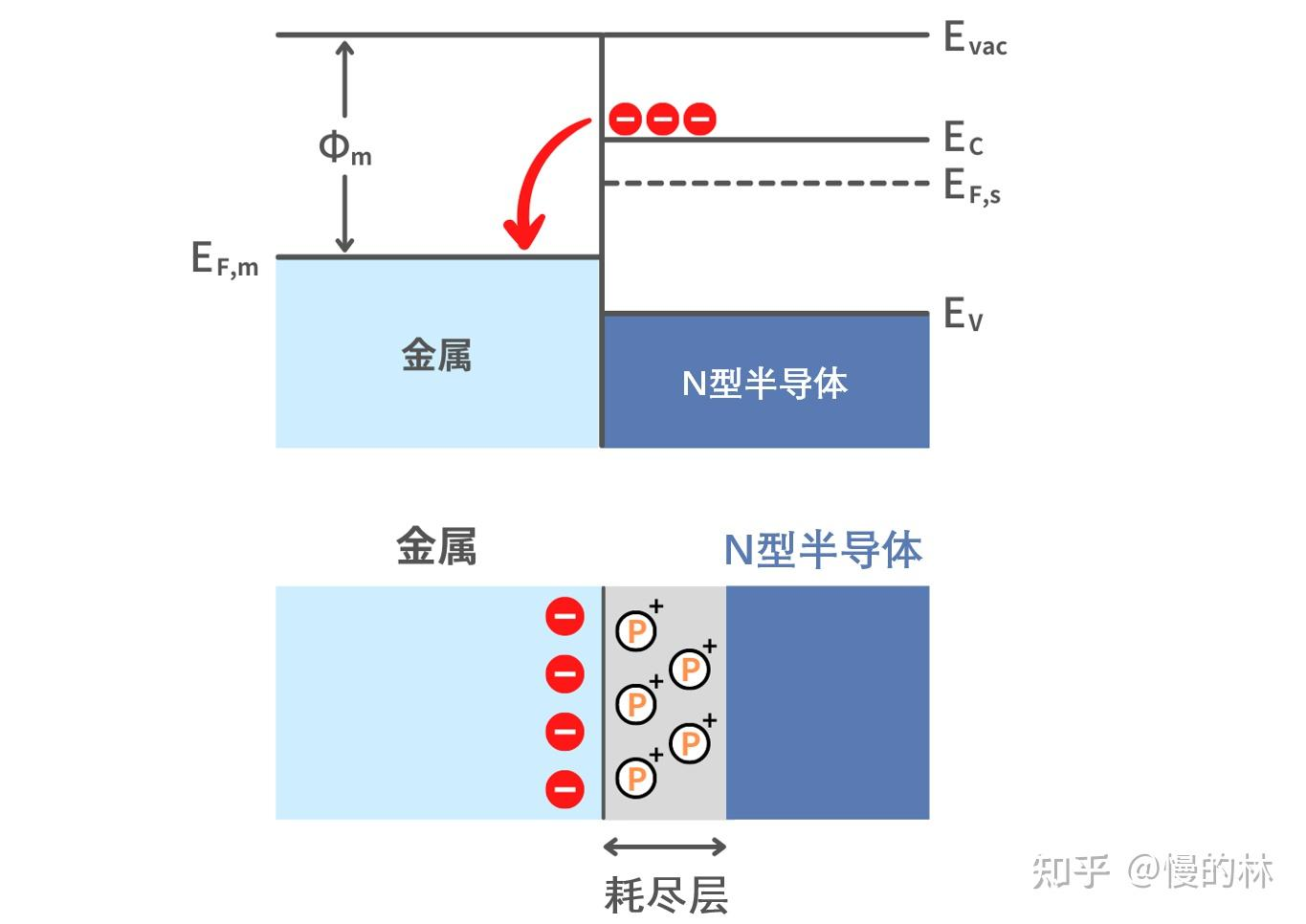
当金属和n型半导体接触时,半导体中的传导电子比金属中的传导电子具有更高的能量,因此接触界面附近的电子向金属移动。金属费米能级基本不变(载流子浓度高),半导体费米能级下降,直到两者之间的能量差消失。
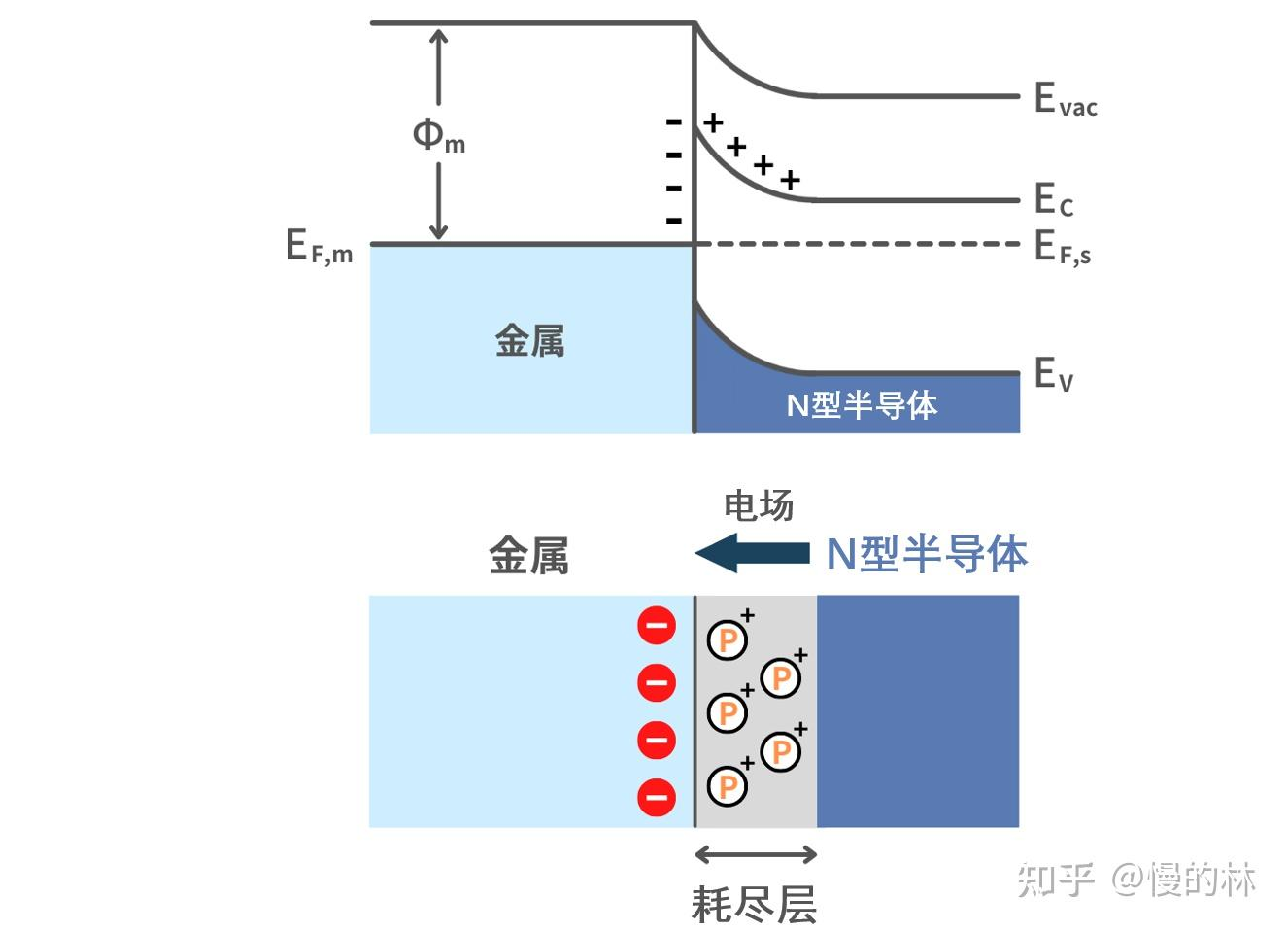
通过接触实现电子转移,半导体带正电,金属带负电,在界面处形成耗尽层,产生从半导体指向金属的电场。
半导体的载流子密度远低于金属,电子运动产生的耗尽层向半导体侧扩展深度大。
半导体中产生的耗尽层和电场充当能量势垒,因此接触面处的半导体能带向上弯曲。
以这种方式产生的电位差称为“内建电压”。它在金属和半导体之间形成势垒,使得电流难以从金属流向半导体。这称为“肖特基接触”。
为什么会能带弯曲
能带代表着电子能量的变化,顺着电势降低的方向也就是电场方向,其能带向上弯曲,电子运动困难,因而其对应的能量需要上升(吸收能量才能跃迁到更高处,这才对应电子运动困难的情况)
至于老师问的为什么这两种接触都是n型半导体或者p型半导体而不是本征半导体:
首先,本征半导体中的载流子浓度跟n型半导体载流子浓度不在一个量级上,很难产生上述所说的,半导体中的电子流入金属这一过程,自然不会产生电势降,也就不会有能带弯折,本征半导体跟金属的接触就相当于金属绝缘体接触。 其次,为什么是n型半导体,n型半导体费米能级靠近导带,majority carriers是电子;p型靠近价带,取决于掺杂浓度,n型高掺杂时费米能级甚至会超过导带。而对于本征半导体,也就是纯净无掺杂的,理论上T=0K的时候费米能级就在价带和导带的中间。
为了避免大体系的DFT计算,我们打算用一个简单的模型来刻画这个band-bending。
一维耗尽近似
考虑最简单的一维耗尽近似,假设耗尽区中自由电子全部进入金属中,只剩下正电荷,正电荷密度是$N_D$,而半导体的体区仍然是施主完全电离,$n\approx N_D$,正电荷密度也是$N_D$,是为中性区。
取界面在 $z=0$,$z>0$ 指向 TiO₂ 体内。
耗尽区(depletion region) $0\le z\le W$:几乎没有自由载流子,只剩下半导体边的正电荷
准中性体区(bulk region) $z>W$:净电荷与电场为0,电势为常数(0)。(边界条件)
$\varepsilon_s=\varepsilon_r\varepsilon_0$(半导体介电常数)、$N_D$(施主浓度)
$\Delta E(z)=-q,\psi(z)$。
耗尽区的电荷密度:
$$
\rho(z)=
\begin{cases}
+qN_D,& 0\le z\le W,\
0,& z>W~.
\end{cases}
$$
耗尽区一维泊松方程:
$$
\frac{d^2\psi}{dz^2}=-\frac{\rho}{\varepsilon_s}=-\frac{qN_D}{\varepsilon_s}
$$
积分一次得到
$$
\psi^{\prime}(z)=-\frac{d\psi}{dz} = -\frac{q N_D}{\varepsilon_s}z+C_1
$$
带入边界条件 $E(W)=-\psi^{\prime}(W)=0$,
$$
C_1 = \frac{qN_D}{\varepsilon}W
$$
得电场:
$$
E(z)=-\frac{d\psi}{dz}=\frac{qN_D}{\varepsilon_s}(z-W).
$$
再积分得到电势:
$$
\psi(z)=-\frac{qN_D}{2\varepsilon_s}(z^2-2Wz)+C_2
$$
$$
\psi(z)=-\frac{qN_D}{2\varepsilon_s}(z-W)^2+C_2
$$
边界条件 $\psi(W)=0$ 得$C_2=0$电势:
$$
\psi(z)= -\frac{qN_D}{2\varepsilon_s}(z-W)^2,\quad 0\le z\le W.
$$
界面到体区的电势降:
$$
V_{\rm bi}=\psi(W)-\psi(0)=\frac{qN_DW^2}{2\varepsilon_s}.
$$
带边上移量(eV到V转换):
$$
\Delta E(z)=-q\psi(z)=
V_{\rm bi}\Big(1-\frac{z}{W}\Big)^2
$$
于是耗尽宽度:
$$
W=\sqrt{\frac{2\varepsilon_s V_{\rm bi}}{q N_D}}
$$
Schottky–Mott势垒:
$$
\Phi_{Bn}=\Phi_M-\chi
$$
其中$\Phi_M$就是金属的功函数(Au),$\chi$:半导体电子亲和势(electron affinity)($\rm TiO_2$),定义为导带底到真空能级的能量。
接触后半导体边体区,也就是能带平了之后的区域有关系:
$$
E_C-E_F \approx k_BT \ln\frac{N_C}{N_D}
$$
其中$N_C$:导带有效态密度,$N_D$:施主浓度。
这个公式来自于教科书Physics of Semiconductor Devices
首先对于费米狄拉克分布:
$$
f(E)= \frac{1}{1+e^{\frac{E-E_F}{k_BT}}}
$$
如果$E_c-E_F\geq3k_BT$,我们有非简并近似,也就是玻尔兹曼近似
$$
f(E)\approx e^{-\frac{E-E_F}{k_BT}}
$$
电子浓度:
$$
n = \int_{E_c}^{\infty}g_c(E)f(E)dE
$$
其中
$$
g_c(E)=\frac{1}{2\pi^2}\left(\frac{2m}{\hbar^2}\right)^{\frac{3}{2}} \sqrt{E-E_c}
$$
带入上式积分,并用玻尔兹曼近似,令 $x=\frac{E-E_c}{k_BT}$可得:
$$
n = e^{-(E_c-E_F)/k_BT}\frac{1}{2\pi^2}\left(\frac{2m}{\hbar^2}\right)^{\frac{3}{2}}(k_BT)^{\frac{3}{2}}\int_0^\infty \sqrt x e^{-x}dx
$$
其中积分
$$
\int_0^\infty \sqrt x e^{-x}dx = \frac{\sqrt\pi}{2}
$$
得到:
$$
n = N_c e^{-\frac{E_c-E_F}{k_BT}}
$$
$$
N_c=2\left(\frac{2\pi mk_BT}{h^2}\right)^{\frac{3}{2}}
$$
在半导体的中性区$n\approx N_D$,对上面 $n$ 取对数即可得
$$
E_C-E_F \approx k_BT \ln\frac{N_C}{N_D}
$$
如果不用玻尔兹曼近似的话,就得用费米积分
$$
n = N_cF_{1/2}(\eta),F_{1/2}(\eta)=\frac{2}{\pi}\int_0^\infty \frac{\sqrt{x}}{1+e^{x-\eta}}dx
$$
其中 $\eta=\frac{E_F-E_c}{k_BT}$
应用以上近似,我们可得内建电势:
$$
V_{\rm bi}\approx\Phi_{Bn}-\frac{E_C-E_F}{q}
$$
取 $E_F$ 为能量零点:
$$
E_C^{\rm bulk}=E_C-E_F,\qquad E_V^{\rm bulk}=E_C^{\rm bulk}-E_g.
$$
空间分布曲线:
$$
E_C(z)=E_C^{\rm bulk}+V_{\rm bi}\Big(1-\frac{z}{W}\Big)^2
$$
$$
E_V(z)=E_V^{\rm bulk}+V_{\rm bi}\Big(1-\frac{z}{W}\Big)^2
$$
于是就可以得到能带弯曲曲线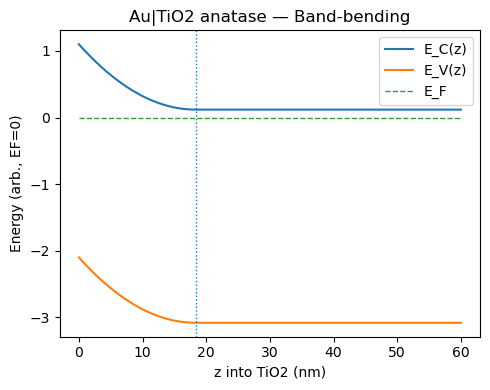
参数设置为:
$N_c$:1e21 这个参数只跟具体材料有关,从公式我们能看出只跟有效质量有关,如果温度一定的话。
$N_D$:1e19 这个就是参杂浓度
$\phi_m$:5.10 eV 金属的功函数,金大概在4.8-5.4eV之间,取决于表面的干净程度
$\chi$: 4eV $\rm TiO_2$的亲合能,导带底到真空能级的位置
$E_g$:3.20eV $\rm TiO_2$的band gap
$\varepsilon_r$: 31 $\rm TiO_2$的介电常数
T:设置为300K
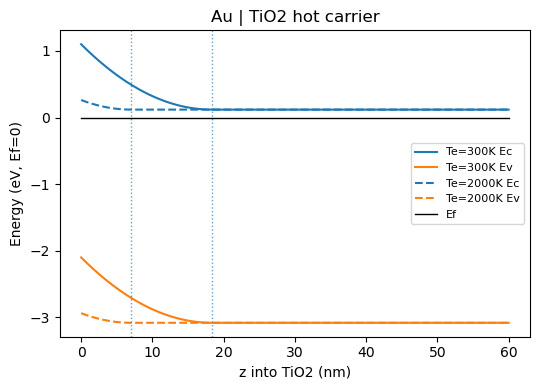
Hot carrier
现在我们考虑Au的hot carrier,激光打在Au上,激发等离子体,等离子体衰减,能量传给电子,产生远高于晶格温度的的电子,所以叫”hot carrier”,之前我们做了一个简单的模型来考虑这样的热电子,也就是算出Au的DOS,然后乘上2000K的费米狄拉克分布,理论上2000K对于Au的化学势会有十几个meV的修正,但在这里不重要,如图所示。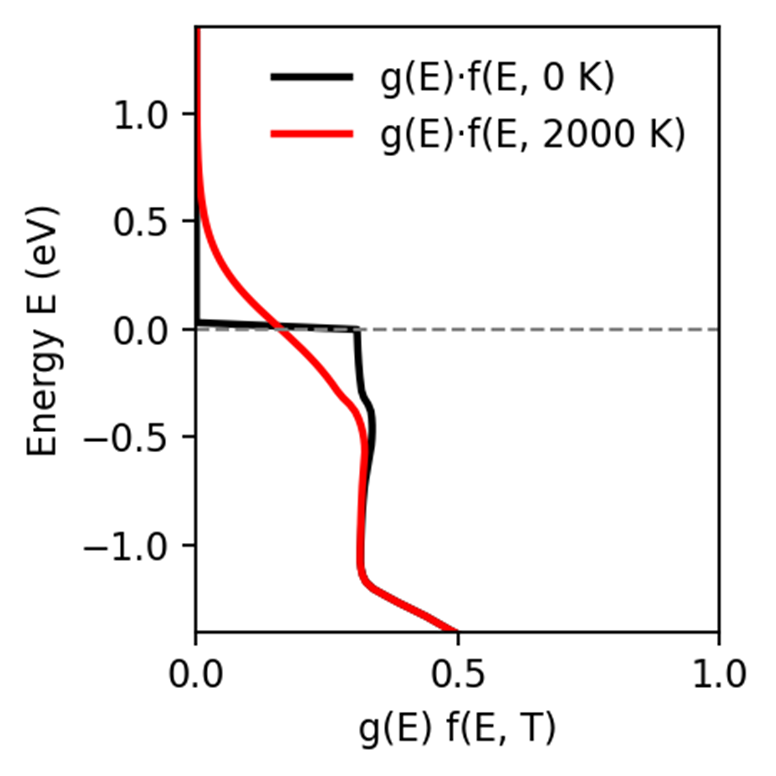
上面我们已经分析了正常的平衡态的金属半导体接触,半导体中的电子流入金属中去,产生耗尽区,形成肖特基势垒,进而能带弯折。现在将热电子考虑进去,简单来想,Au的的高能电子会有一部分跨过这个势垒,回到半导体体带,中和一部分耗尽区的正电荷,削减耗尽区的宽度,能带弯折程度减弱,
如何将金属边的图像和半导体边的物理图像拼起来?
Physics of Semiconductor Devices 中提到,热发射(Thermionic-Emission)电流密度:
$$
J_{S\to M} \sim A^{} T_s^{2} \exp\left[-\frac{q(\Phi_{B_n} - V)}{k_B T_s}\right]
$$
这里V是外加偏置电场,A是常数
$$
J_{M\to S} \sim A^{} T_e^{2} \exp\left(-\frac{q \Phi_{B_n}}{k_B T_e}\right)
$$
净电流就是两者之差,在这里我们标记了Ts是半导体侧的晶格温度,Te是金属热电子温度,在不考虑外加偏置电场的时候,且两者温度一致的时候,显然静电流为0,两者相等。但现在考虑hot carrier,金属一侧的电子温度高于半导体一侧,就产生电流,电子流向半导体,与耗尽区正电荷中和之后动态平衡,然后静电流又为0,这时候我们可以看作产生了一个正向偏置电压,最后平衡的时候两个电流相等。这时可以解出:
$$
V_{hot}= \frac{2 k_B T_s}{q} \ln\frac{T_e}{T_s}+ \Phi_{B_n} \left(1 - \frac{T_s}{T_e}\right)
$$
这一电势相当于修改我们前面的内建电场$V_{bi}$
$$
V_{eff} = V_{bi} - V_{hot}
$$
耗尽区的宽度变为:
$$
W=\sqrt{\frac{2\varepsilon_s (V_{\rm bi}-V_{hot})}{q N_D}}
$$
变窄,如图所示。